Indice dei contenuti
ToggleArticolo di Mattia Favretto – Full-stack Developer in AzzurroDigitale
Scopriamo come è possibile stampare oggetti solidi minimizzando gli sprechi di materiale e aumentando l’efficienza produttiva grazie ad un avanzato software di nesting.
Nel mondo della manifattura, lo spazio è denaro. Ogni centimetro quadrato di materiale sprecato o di volume non utilizzato si traduce in una perdita diretta. Qui entra in gioco il Nesting: non solo un semplice incastro di forme, ma una complessa sfida matematica volta a minimizzare gli sprechi.
Esistono diverse tipologie di nesting. Il più comune è il Nesting 2D, tipico del taglio lamiere o tessuti, dove figure piane vengono disposte su una superficie. All’estremo opposto c’è il Nesting 3D, in cui si cerca il miglior posizionamento per figure solide, estremamente complesso computazionalmente.
Nel mezzo, però, esiste una sfida specifica che abbiamo affrontato: il Nesting 2.5D. In questo scenario, partiamo da oggetti tridimensionali (file CAD) che devono essere disposti su un piano, ma la cui disposizione è vincolata non solo dalla loro impronta a terra, ma anche dalle loro altezze e caratteristiche geometriche spaziali. La letteratura scientifica è vasta, ma spesso teorica; implementare una soluzione industriale richiede di superare la barriera tra teoria accademica e realtà produttiva.
L’adozione di un algoritmo di nesting avanzato non è un vezzo tecnologico, ma una leva strategica per la competitività.
- Standardizzazione della qualità: Mentre l’efficienza umana può variare in base alla stanchezza o all’esperienza, l’algoritmo garantisce una ricerca costante della soluzione ottima, assicurando risultati prevedibili e ripetibili.
- Riduzione dei costi diretti: L’obiettivo primario è ridurre lo spreco di materia prima. Ottimizzando il posizionamento dei pezzi, si riescono a inserire più prodotti nella stessa lastra o nello stesso volume di carico, riducendo drasticamente il materiale di scarto (waste).
- Automazione e velocità: Processi che richiederebbero ore di tentativi manuali da parte di operatori esperti vengono risolti in un tempo ridotto, liberando risorse umane per compiti a maggior valore aggiunto.
How It Works: semplificare la complessità
Immaginate di giocare a Tetris, ma con regole molto più difficili: i pezzi non sono semplici blocchi geometrici, ma forme irregolari curve e complesse.
La nostra soluzione affronta il problema in tre fasi logiche:
1.Prevenzione delle collisioni (Marginatura di Sicurezza): Prima di incastrare i pezzi, il software aggiunge un piccolo cuscinetto, un margine di sicurezza attorno al perimetro di ogni sagoma. Questo accorgimento serve non solo per esigenze produttive ma anche a compensare piccole imprecisioni matematiche ed evita che i pezzi si tocchino o si sovrappongano accidentalmente durante il posizionamento.
2.Riconoscimento (dal 3D al 2D): Il sistema non vede solo una sagoma piatta. Analizza il file CAD originale (formato STEP) e ne estrae l’impronta a terra (il perimetro esterno), tenendo traccia anche delle delle altezze. È come se facessimo una radiografia dell’oggetto per capire quanto spazio occupa realmente.

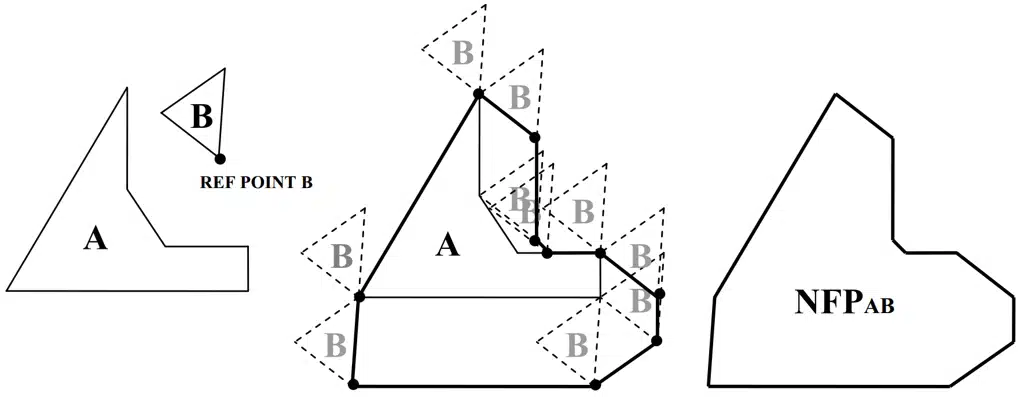
3.Geometria NFP: Per capire se due pezzi si incastrano, il software calcola un’area matematica “proibita” attorno a ciascun pezzo già piazzato (A). Se il nuovo pezzo (B) entra in quest’area, significa che c’è una collisione, se il nuovo pezzo tocca il bordo dell’area avremo un contatto perfetto. L’obiettivo è far scivolare il nuovo pezzo il più vicino possibile a quelli esistenti senza mai entrare nella zona proibita.
4.Il gioco dell’ottimizzazione: Una volta capito come incastrare due pezzi, bisogna decidere quale pezzo inserire e dove. L’algoritmo prova migliaia di combinazioni diverse: ruota i pezzi, cambia l’ordine di inserimento e “scuote” la soluzione quando si accorge di essere bloccato, tutto per trovare la configurazione che occupa meno spazio possibile.
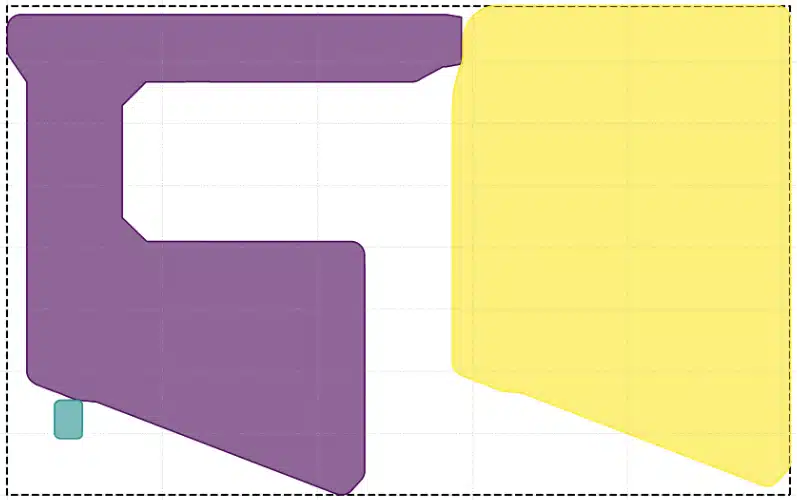
Gli oggetti qui rappresentati contengono un bordo di sicurezza per cui non si toccano anche se sono vicini
Deep Tech per gli addetti ai lavori
La nostra implementazione tecnica è scritta in Python e sfrutta librerie avanzate per la manipolazione geometrica e l’ottimizzazione euristica. Considerando che il nesting è una variante del problema Bin Packing, classificato come NP-Hard (quindi con complessità non polinomiale), nella ricerca del risultato occorre ricorrere ad una soluzione sub-ottima dal momento che la ricerca della soluzione migliore richiederebbe un tempo eccessivo, non applicabile per il nostro caso.
1. Elaborazione CAD e Generazione 2.5D
La sfida inizia con file STEP grezzi. Utilizziamo la libreria PythonOCC per importare la geometria 3D e analizzarla.
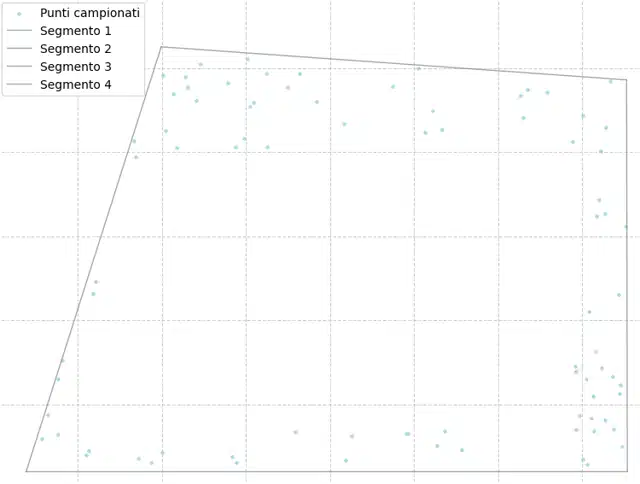
- Proiezione e Alpha Shape: L’algoritmo campiona punti lungo i bordi delle facce del modello 3D e li proietta sul piano base. Su questi punti viene calcolato il perimetro della figura.
- Mappatura delle altezze: Non ci limitiamo al perimetro per capire quanto è alto l’oggetto. Vengono identificati i segmenti che meglio semplificano la nostra figura e per ognuno di essi ne calcoliamo l’altezza, tenendo in considerazione anche la geometria del poligono; questo permette di valutare correttamente le possibili variazioni di altezza presenti in un singolo pezzo. In particolare costruiamo un area rettangolare per ogni lato e prendiamo randomicamente dei punti dei quali calcoliamo l’altezza, usando poi una media pesata superiore (è meglio sbagliare per eccesso che per difetto) associamo ad ogni lato un’altezza.
2. Il cuore geometrico: No-Fit Polygon (NFP)
Per il posizionamento, utilizziamo il concetto di No-Fit Polygon (NFP)1. Invece di controllare in continuazione se il nuovo pezzo si scontra con quelli già posizionati, il software genera prima una sagoma speciale. Questa sagoma, che si basa su un calcolo geometrico chiamato Minkowski Difference, rappresenta l’esatto spazio vietato attorno ai pezzi fissi. In pratica, è l’impronta che il nuovo pezzo lascerebbe se si muovesse lungo i bordi di quelli già piazzati, indicando le posizioni di contatto perfetto.
Utilizziamo la libreria Pyclipper per eseguire queste operazioni booleane complesse in modo efficiente.
La zona NFP risultante rappresenta l’insieme di tutte le posizioni in cui il centroide del pezzo mobile non può andare. Di conseguenza, i contorni di questa zona rappresentano le posizioni di contatto perfetto.
L’algoritmo seleziona i candidati migliori dalla geometria NFP, privilegiando posizioni Bottom-Left per compattare il layout verso l’origine e ridurre lo spreco. La scelta delle posizioni valide per i pezzi deve tenere conto del vincolo di altezze, viene fatta quindi una ricerca dei pezzi adiacenti e nel caso in cui l’altezza di questi sia eccessivamente diversa viene applicata una penalità alla soluzione trovata, tanto maggiore quanto maggiore è la differenza di altezza, permettendo quindi a soluzioni le cui altezze sforano di poco il limite imposto di non essere completamente scartate.
3. Algoritmo di ottimizzazione GLS (Guided Local Search)
Non ci affidiamo a un semplice approccio greedy. Abbiamo implementato una meta-euristica Guided Local Search (GLS).
Mutazioni Locali: L’algoritmo esplora lo spazio delle soluzioni applicando mutazioni alla sequenza originale attraverso rotazioni, scambio di pezzi e di gruppi di pezzi.
Gestione dei vincoli: L’algoritmo applica dei costi maggiori alle soluzioni che violano i vincoli di altezza fissati, rendendole più sfavorevoli ma comunque possibili nel caso in cui lo spreco sia comunque molto basso.
Restart e Perturbazione: Per evitare minimi locali, il sistema monitora i miglioramenti. Se dopo un certo numero di iterazioni non si trova una soluzione migliore, viene innescata una permutazione massiccia. Questa fase mischia completamente la sequenza e assegna rotazioni casuali, forzando l’algoritmo ad esplorare una zona completamente nuova dello spazio delle soluzioni, accettando temporaneamente anche soluzioni peggiori per uscire dallo stallo.
Glossario del developer
- No-fit polygon (NFP): È l’area proibita che si forma attorno a un pezzo già piazzato (A), all’interno della quale il punto di riferimento di un nuovo pezzo (B) non può entrare. Posizionando il punto di riferimento di B:
Per creare la NFP nel nostro algoritmo si utilizza il centroide del pezzo, questa però può essere calcolata rispetto a ciascun punto di riferimento del pezzo B.
Sul bordo dell’NFP: i pezzi A e B sono a contatto perfetto (incastro).
All’interno dell’NFP: i pezzi A e B si sovrappongono (collisione).
Per poter minimizzare l’area occupata nel piazzamento del pezzo B sceglierò come posizione un punto sul bordo del NFP. ↩︎